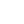Jakarta, CNN Indonesia –
Segitiga adalah bangun datar yang mempunyai sudut dan rusuk yang berpotongan. Jika sudut suatu segitiga berubah maka panjang sisinya juga akan berubah.

Dalam trigonometri, menghitung sisi-sisi segitiga mudah dilakukan jika Anda mengetahui sudut tertentu. Jadi, apa yang dimaksud dengan sudut istimewa? Berikut penjelasan dan contoh soalnya.
Itu didefinisikan dari sudut tertentu
Diperoleh dari Buku Ajar Kelas SMA/MA
Sudut yang dimaksud adalah 0°, 30°, 45°, 60°, dan 90°. Sudut-sudut ini disebut istimewa karena hanya dengan sudut-sudut tersebut mereka dapat dengan cepat menghitung besar atau panjang salah satu sisi suatu segitiga tanpa perlu menghitungnya.
Sudut istimewa banyak terdapat pada segitiga yang sering dipelajari dalam matematika dan fisika. Dalam kehidupan sehari-hari kita bisa melihatnya di gedung, meja, rak, dll.
Tabel trigonometri sudut istimewa dan perbandingannya
Saat mempelajari sudut istimewa, kita pasti akan menuju ke tabel sudut istimewa. Suku-suku tersebut merupakan hasil atau rangkuman perbandingan nilai trigonometri sudut tertentu, misalnya sudut 0° hingga sudut 90°.
Tabel trigonometri sudut khusus dirancang untuk mempermudah penyelesaian masalah. Tabel ini menunjukkan nilai sin, cos, dan tan dari sudut tertentu.
Trigonometri relatif pada tabel di atas merupakan hasil akhir yang diperoleh dari pengukuran sama kaki dan segitiga berikut. 1. Perbandingan trigonometri sudut 0° Sin 0° = BC/AC = 0/AC = 0 Cos 0° = AB/AC = 1/1 = 1 Tan 0° = BC/AB = 0/AB = 0 2. Rata-rata trigonometri sudut 30° Sin 30° = AD / AC = s / 2 : s = 1/2 Cos 30° = CD / AC = s / 2 √3 : 2 = 1/2 √3 Tan 30° = AD / CD = s /2 : s/2 √3 : 2 = 1/3 √3 3. Besaran trigonometri sudut 45° Sin 45° = BC / AC = s / 2 : s = 1/2 √2 Cos 45° = AB / AC = s/ s√2 = 1/2 √2 Tan 45° = BC/AB = s/s = 1 4. Nilai perbandingan trigonometri sudut 60° Sin 60° = CD /AC = s/2 √3: s = 1/2 √3 Cos 60° = AD/AC = s/2 : s = 1/2 Tan 60° = CD/AD = s/2 √ 3: s/2 = √ 3 5. Perbandingan trigonometri sudut 90 ° Sin 90° = BC / AC = 1 Cos 90° = AB / AC = 0 / AC = 0 Tan 90° = BC / AB = BC / 0 = tidak terdefinisi
Contoh soal sudut khusus
Untuk lebih memahami cara menggunakan sudut tertentu, berikut contoh soal yang bisa Anda pelajari. Jangan lupa gunakan kata kunci di atas agar mendapatkan hasil dengan mudah. 1. Hitung nilai sin(45°) + cos(45°) + tan(45°)
Menjawab:
Dari tabel tersebut terlihat bahwa sin(45°) = 1/2√2, cos(45°) = 1/2√2, dan tan(45°) = 1.
Jadi, sin(45°) + cos(45°) + tan(45°) = 1/2√2 + 1/2√2 + 1 = √2 + 1 2. Hitunglah nilai sin(30° ) + cos (30°) – sin(60°)
Menjawab:
Sin(30°) = 1/2, cos(30°) = 1/2√3, sin(60°) = 1/2√3
Jadi, sin(30°) + cos(30°) – sin(60°) = 1/2 + 1/2√3 – 1/2√3 = 1/2 3. Hitung nilai tan 60° sin 90 ° – 30 ° atau 60 °
Menjawab:
Tan 60° sin 90° – detik 30° cos 60°
Persamaan = (√3 x 1) – (1/2√3 x 1/2) = √3 – 1/3√3 = 2/3√3
Demikianlah penjelasan sudut spesifik dan contoh soal yang bisa kamu pelajari. Semoga membantu. (Nyonya/Juh)